｜文／Eric Chuang｜原文出處／applemint Ltd. – A/B 測試要測多久？從統計顯著與檢定力看廣告測試結果｜首圖／Freepik
上次，我們在〈如何評估網路廣告成效？統計樣本與誤差預測網路廣告投放效果〉一文中，說明了統計學中誤差與母體的概念。
今天，我們將進一步介紹另外一項與 A/B 測試有關的觀念：顯著性 (significance) 與檢定力 (power)。
也許看完上一篇文章，你會開始認為：根本沒辦法執行 A/B 測試了，因為沒有足夠的預算。但做 A/B 測試的目的，其實是為了要在不同版本中的廣告中，找出「更適合」的「最佳版本」。
因此，即使沒有 200 萬預算，只要你的每次測試的預算在 50000 元以上，那麼執行 A/B 測試還是可行的。下面用檢定力與顯著性來說明原因——決定 A/B 測試所需要的樣本數。
結論來說，在執行 A/B 測試前，你必須先知道：
- 你能夠容許的誤差範圍如何，容許範圍越小，需要越多樣本
- 測試標的預計帶來的成效差異如何，差異越小，需要越多樣本
這篇文章，會透過統計學中的「統計顯著性」與「統計檢定力」的概念，以及 2 個可以協助計算檢定力的工具，讓沒有太多統計基礎的數位行銷人員，也能了解 A/B 組合是否有顯著差異。
本篇目錄
廣告成效與統計顯著性的關係
我們在〈廣告要跑多久〉一文中曾提到，同樣 10% 的轉換率，100 人中 10 人轉換，與 1000 人中 100 人轉換意義不同。
今天，我們設想另一個情境：點擊率 1% 跟點擊率 2%，哪個成效比較好？
你猜對了嗎？答案是：我們不知道。
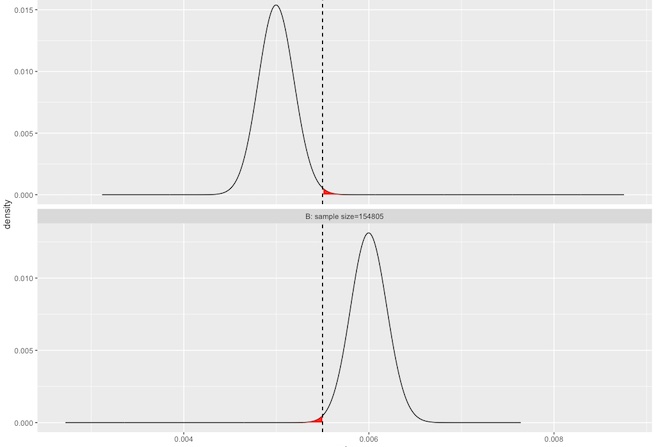
如果是 100 次廣告曝光中有 1 次點擊，以及 200 次曝光中有 4 次點擊，我們並沒有辦法得出「點擊率 2% 比較好」的結論。
但如果是 2,500 次曝光中有 25 次點擊，對上 2,500 次曝光中有 50 次點擊，那麼情況就不一樣了，我們有更多的信心可以說點擊率 2% 比較好。
廣告投放與統計學中的假設檢定
在統計學中，有兩種推論結果的方式，其中一種是顯著性檢定 (significance test)，另一種則是檢定力分析 (power analysis)。這與統計學中的「假設 (hypothesis)」有關，我們這邊直接用廣告的例子來說明以上三種概念。
什麼是假設？
在推論統計中，會出現虛無假設 (null hypothesis) 與對立假設 (alternative hypothesis) 兩種假設。有關兩種假設的詳細定義，可以參考統計學的課程內容，或是網路上討論的相關文章。
一般來說，虛無假設指涉的會是「現況」或是「沒有採取任何措施的結果」，對立假設是我們希望證明的結果（拒絕虛無假設）。
以數位廣告投放 A/B 測試的情境來說，我們可以做出以下的假設：
虛無假設
A 版本與 B 版本的點擊率/轉換率相同*
*「相同」是簡化的說法，較正式的說法是「A 版本的結果與 B 版本的結果來自同一個母體」。
對立假設
A 版本與 B 版本的點擊率/轉換率不同
以上是雙尾檢定的例子，關於單雙尾檢定的討論不在本次主題範圍，因此不加贅述。
什麼是顯著性檢定？
顯著性關注的議題是，我們根據觀察結果所做出來的推論，有多少機會可能是「錯誤的拒絕虛無假設」。
以上述的例子來說，就是代表「明明點擊率相同 (虛無假設)，但我們說不同 (對立假設)」的機率。
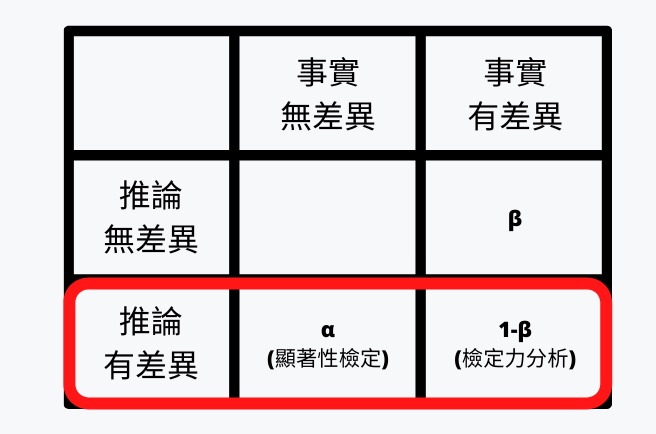
統計學中最喜歡用的例子，是「明明無罪 (虛無假設)，卻被判為有罪 (對立假設)」的情況，這種錯誤在統計學中，稱為 Type I Error。
顯著性檢定的結果，通常會用 p 值 (p-value) 或 α 來表現，一般標準要小於 0.05，代表「錯誤的拒絕虛無假設」機率低於 5%。
什麼是檢定力分析？
根據原始定義，是「沒有錯誤接受虛無假設 (β) 」的機率。以我們前面提到的例子來說，就是「明明有罪，卻誤判成無罪的情況」、「明明點擊率有差異，卻說點擊率一樣」。
檢定力分析根據觀察到的結果做出推論，也就是「正確拒絕虛無假設 (1-β) 」的機率 。
一般來說，我們會希望統計檢定力在 80% 以上。以簡化的方式來理解，就是我們希望對「 A 版本與 B 版本點擊率/轉換率不同的推論，有 80% 的機會是正確的」。
在了解統計學中「檢定」的三個重點後，我們接下來就要說明如何將統計學的概念，落實到廣告投放的 A/B 測試上。
評估廣告 A/B 測試
在執行 A/B 測試時，我們需要解答兩個問題：
- 從這次的實驗結果來看，A 版本與 B 版本是否有明顯差異？
- 從過去經驗來看，新的測試應該需要多少樣本才夠？
以下將分別說明：
A 版本與 B 版本的顯著性檢定
我們可以利用 AB Testguide 提供的工具來檢測兩組廣告或兩組受眾之間的差異是否達到顯著。
以前面的例子來說，當我們的樣本數分別只有 100 與 200 次曝光的時候，我們會得到的結果沒有顯著性：
兩者之間並沒有顯著差異。
但如果是個別有 2500 次曝光時，便會得到有顯著性的結果：
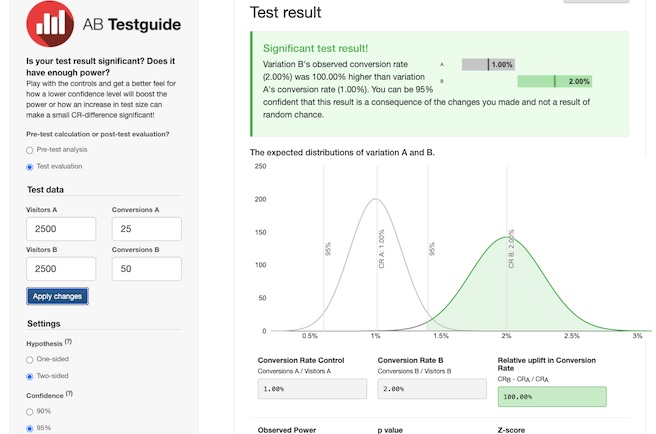
A/B 測試樣本數量需要多少？
以檢定力與顯著性決定。
當我們的廣告進行了一段時間後，我們需要知道需要多少樣本來進行 A/B 測試。此時我們就能透過 ClinCalc 提供的計算工具。
在進行 A/B 測試時，我們需要選擇的是兩個獨立群組的比較。由於點擊與轉換只有兩種結果 (點/不點、買/不買)，因此計算上我們會選擇二分法 (Dichotomous)。
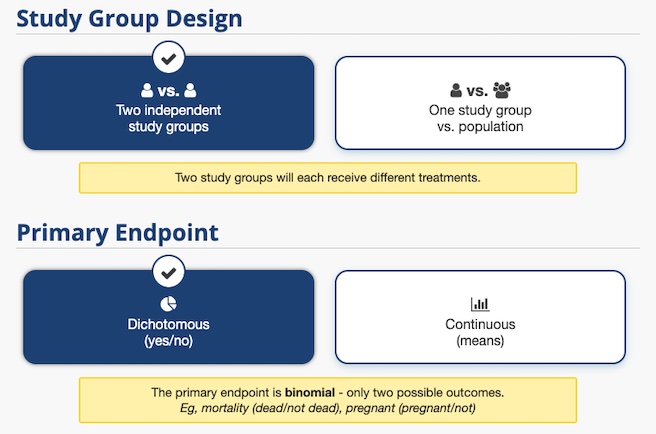
我們預計這次的測試，要讓點擊率從 1% 改善到 2%，因此 Group 1 填寫現況的 1%，Group 2 則填寫預計的 2%。
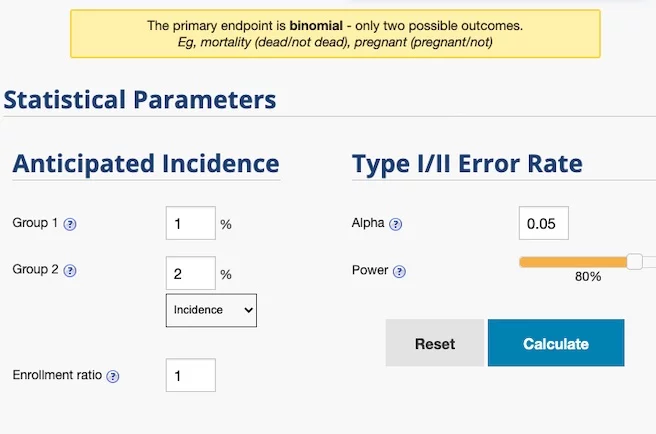
計算後得知，我們的測試各自需要曝光至少 2318 次。
因為是範例，所以我們使用了較極端的情境。如果是一般點擊率的差異 (1% 與 1.1%)，保守預估應該要各自曝光 163095 次。如果以 CPM 300 元台幣來算的話，需要 48,928.5 元的預算來執行這次測試。
結論：樣本數不夠的差異都沒有意義
透過今天的文章，我們了解到點擊率 1% 與點擊率 2%，在不同的曝光次數底下，意義完全不同。
利用上述的工具能讓我們知道，當我們希望測試 1% 到 1.1% 之間的點擊率差異時，預計需要投入多少預算、曝光多少次，才能得到有意義的推論。
事實上，不論是 Facebook 的 A/B 測試功能，或是 Google Optimize 在計算轉換率差異時，也是透過顯著性與檢定力，來判定兩種版本是否有「有意義的差異」。
因此，執行 A/B 測試時，了解「能夠接受的誤差範圍」非常重要，唯有將誤差納入考量，才能正確的判讀測試結果。
本次的內容，一方面是為了向各位公開 applemint 實際上會如何判讀客戶的成效，另一方面則是希望透過公開的方式，讓我們的服務品質能夠受到公開的考驗。因此如果發現任何計算或觀念有誤的地方，歡迎隨時與我們聯繫，你們的建議會是我們改進的動力。
如果希望隨時掌握最新的數位行銷文章，也歡迎訂閱 applemint 的電子報。我們每兩週會發布精選文集，讓你隨時掌握 applemint 的最新文章！
附錄：數值的實際計算方法
這裡附上為了進一步了解計算過程，所需要理解的數值計算方式，給有興趣的人做參考。
不必了解附錄全部的內容，也能夠藉由上述的工具進行初步的估算，因此如果自認對於數學或統計有排斥的朋友，可以直接跳過這一部分。
1. 「點擊率」的平均值
我們來設想以下的情況：A、B、C 素材的點擊率分別為 1.2%、0.9% 與 1.05%，請問平均的點擊率是多少呢？
答案一定不是 (1.2+0.9+1.05)/3。
這是因為點擊率是比例，會根據分母的不同而有變化，因此平均點擊率應該是 (A + B + C 素材點擊) / (A + B + C 素材曝光)。
在廣告後台中，我們便把最後得到的彙總值視為是平均值。也就是說，我們把廣告後台「過去 7 天的總點擊率」，當成是「過去 7 天點擊率的平均值」。
2. 「點擊率」的標準誤差 (Standard Error)
標準差與標準誤的計算，需要先計算觀測值與平均值的離差平方和，也就是計算個別點擊率與平均點擊率的差距。但是我們在廣告後台看到的，是整體成效的彙總值，因此不能直接計算。
由於點擊率是二分法 (點與不點)，因此我們可以透過平均點擊率，來計算點擊率的標準誤差。計算方法是：
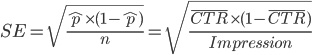
3. 顯著性測試
由於我們的點擊與非點擊的人數都超過 10 (在統計學上即是 np 與 n(1-p) 都大於等於 10)，因此我們在計算兩組分配差異時，可以用以下方式計算兩組平均值差異的標準誤差：
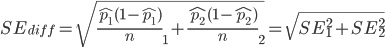
由於樣本數量大於 30，基於中央極限定理，我們推定符合 A 版本與 B 版本皆符合常態分佈，因此使用 Z 分數進行檢定：
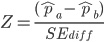
在 Z 檢定中，如果 Z 分數大於 1.96，或是小於 -1.96，便具有統計上的顯著性。
4. 從檢定力推估需要的樣本數
根據 ClinCalc 使用的計算方式，其估算樣本數的計算方式如下：
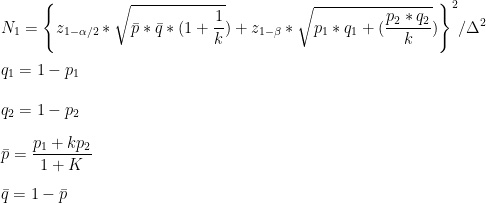
其中兩個 Z 分數要透過查表的方式取得。1-𝛼/2 代表的是雙尾檢定中的 Z 分數，以 p-value 為 0.05 來說，便是 1.96。1-β 則是檢定力對應的 Z 分數，以 0.8 來說，Z 分數為 0.84。Δ 則代表變化的幅度，以點擊率 1% 與 1.05% 為例，Δ 便是 0.05%。
參考資料
學習更多行銷人文章
A/B 測試(a/b testing)教學 – 2021年介紹, 流程, 廣告投放, 推薦工具
廣告數據有哪些？6大廣告數據類型、優缺點比較(可代替Cookie)
｜本文由 applemint Ltd. 授權提供，僅反映專家作者意見，未經原作者授權請勿轉載。
作者資訊
- 歡迎成為《行銷人》合作夥伴，若有任何文章授權、尋求報導及投稿的需求，歡迎來信：[email protected]
此作者最新相關文章
- 2024-12-02數位轉型鳳梨葉翻轉時尚!優織隆勇奪2025台灣精品獎，領航全球永續新趨勢
- 2024-11-29健康專欄術後還是鼻塞? 小心尾端鼻中隔彎曲或空鼻症惹的禍
- 2024-11-22數位轉型潤之泉推出全新「優蛋白滴積精」 全台首創純黑豆發酵素雞精 引領健康新風潮
- 2024-11-21生活時事免安裝！YouTube 下載網站 iMyFone TopClipper，支援多平台下載影片
